これまでの記事で2進数について解説してきましたが、今回は2進数の足し算についての解説です。簡単のため2進数1桁の足し算を考えます。
2つの2進数1桁の数字A(0と1)とB(0と1)があり、AとBの足し算S=A+Bを行います。考えられる組み合わせは下記の通りです。
①:S=0+0=0 (0と0を足しても0)
②:S=0+1=1 (0と1を足すと1)
③:S=1+0=1 (1と0を足すと1)
④:S=1+1=10 (1と1を足すと桁があがり10)
上記④で、桁数を考えない場合は、計算結果が10となりますが、ここでは桁数を1桁としていますので、計算結果はS=0で、桁あがり(キャリーC)が1となります。これを真理値表で表すと表1のようになります。
| 入力 | 出力 | |||
| A | B | S | C | |
| ① | 0 | 0 | 0 | 0 |
| ② | 0 | 1 | 1 | 0 |
| ③ | 1 | 0 | 1 | 0 |
| ④ | 1 | 1 | 0 | 1 |
前回までで説明したAND回路とXOR回路を使って、表1の真理値表をロジック回路で実現すると図3のような回路となり、これを半加算器といいます。図3の回路図のAとBに0か1を入力し、SとCが表1のようになることを確認してください。
 |
| 図3 半加算器※1 |
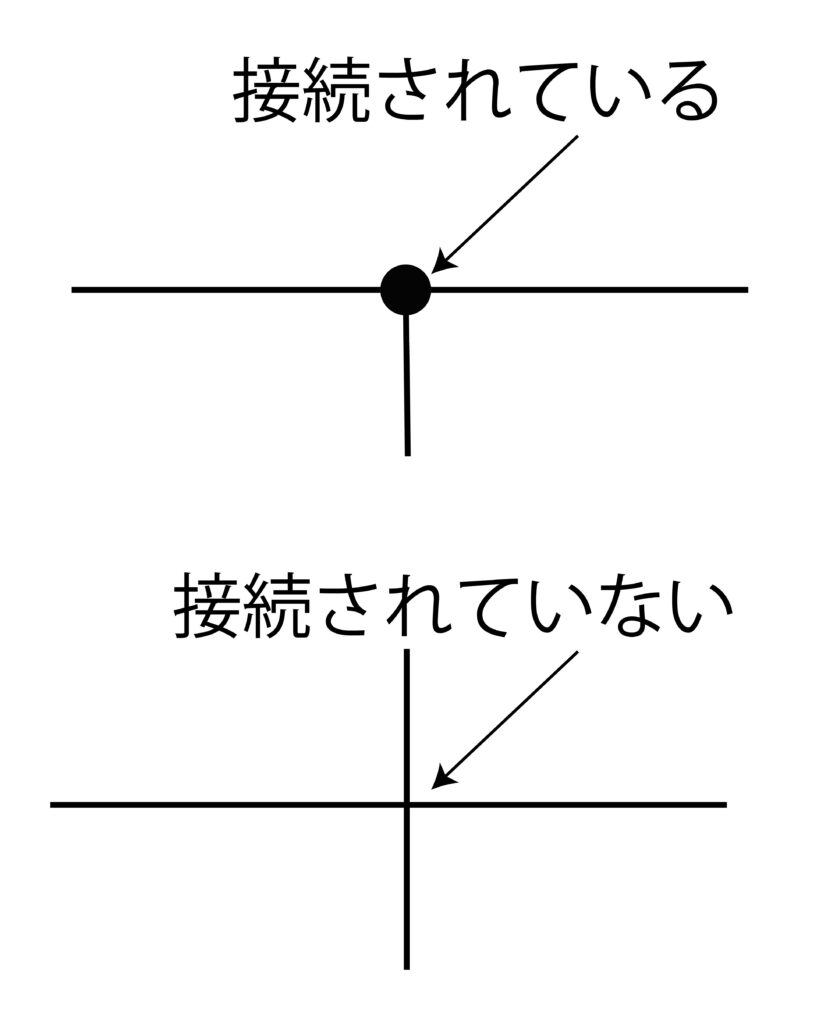 |
| 図4 回路図の約束事 |
半加算器は上の桁への桁上げしか扱えませんが、下の桁からの桁上げを処理できる全加算器があります。全加算器は半加算器で構成されます。また、全加算器を複数接続することで、複数桁の2進数足し算が可能になります。これらの加算器はマイコンに内蔵され、ソフトウェアからの指示に従った演算に使われます。
※1 直線が交わる箇所に黒丸が記入されている部分は結線が接続されており、黒丸が無い部分は接続されていません。(図4参照)