全加算器を半加算器で構成する。ITへの扉(入門編) No.37
2022年12月1日カテゴリー:
ITへの扉
前回、2進数1桁の足し算に半加算器(Half adder)を使用することを述べました。また、1桁の足し算ではほとんど役に立たないため、全加算器(Full adder)を必要な桁数分だけ接続することで、複数桁の2進数の足し算を実現できることを述べました。
全加算器は、前回に述べた半加算器(図4(a))で構成することができます。半加算器の真理値表は表1の通りです。半加算器で構成した全加算器の回路図を図5に示します。全加算器の真理値表は表2の通りです。
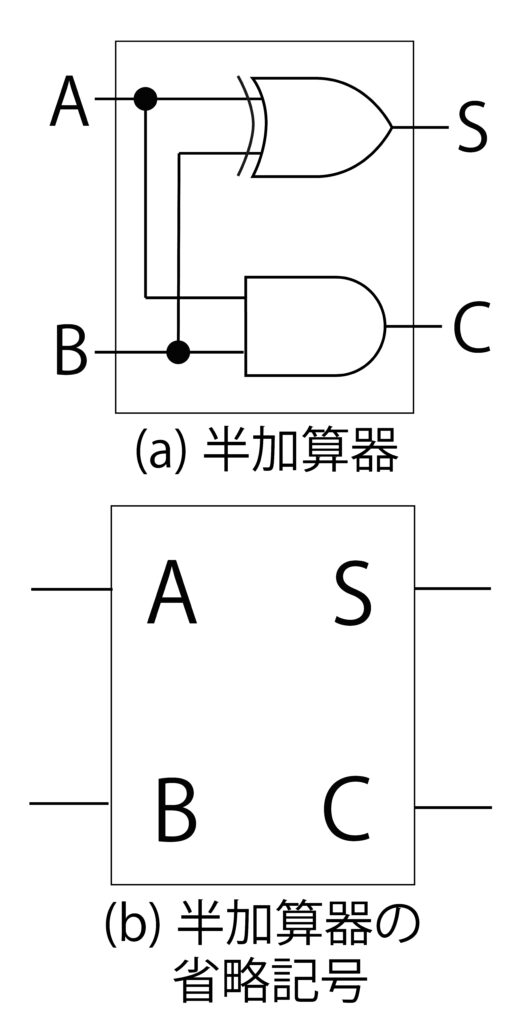 |
| 図4 半加算器 |
表1 半加算器の真理値表
| 入力 |
出力 |
| A |
B |
S |
C |
| 0 |
0 |
0 |
0 |
| 0 |
1 |
1 |
0 |
| 1 |
0 |
1 |
0 |
| 1 |
1 |
0 |
1 |
全加算器は下の桁からの桁上がり(X)や上の桁への桁上がり(C)が処理できます。
表1の半加算器と表2の全加算器のそれぞれの真理値表を見ながら、図5の回路の動作を確認すると頭の体操になるのではと思います。
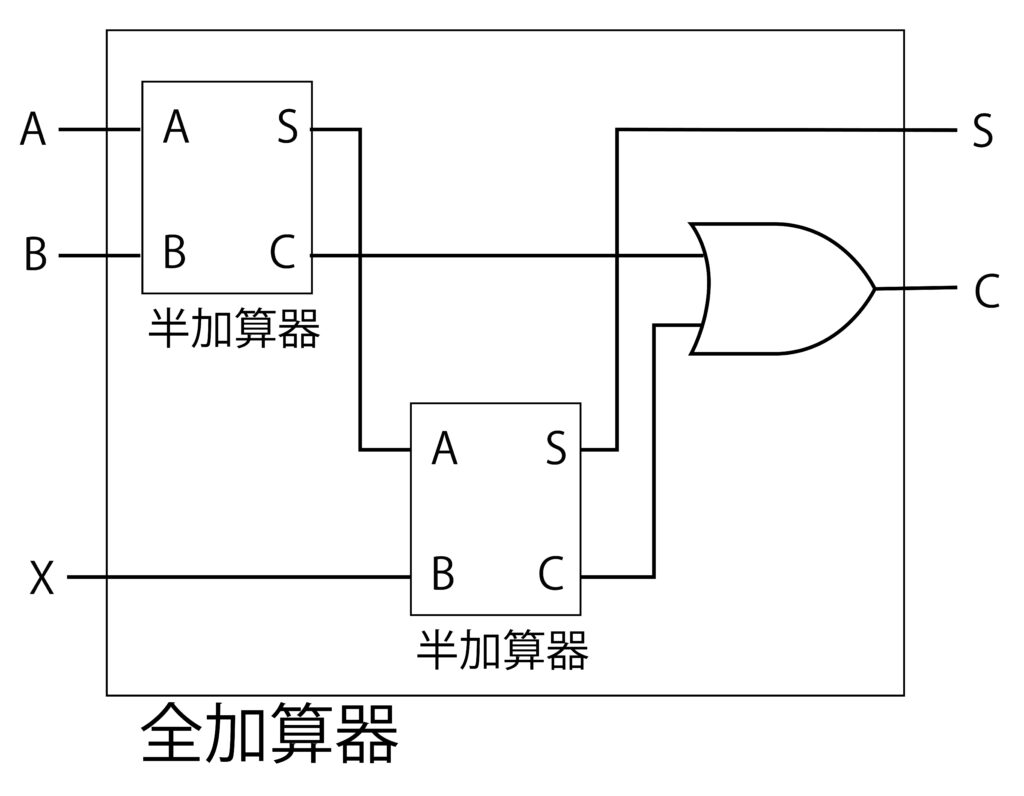 |
| 図5 全加算器 |
表2 全加算器の真理値表
| 入力 |
出力 |
| A |
B |
X |
S |
C |
| 0 |
0 |
0 |
0 |
0 |
| 0 |
0 |
1 |
1 |
0 |
| 0 |
1 |
0 |
1 |
0 |
| 0 |
1 |
1 |
0 |
1 |
| 1 |
0 |
0 |
1 |
0 |
| 1 |
0 |
1 |
0 |
1 |
| 1 |
1 |
0 |
0 |
1 |
| 1 |
1 |
1 |
1 |
1 |
2進数の複数桁の足し算では、全加算器を必要とする桁の数だけ接続すると前述しましたが、実際には、1桁目は下の桁からの桁上がりがないため、半加算器を接続し、2桁目以降に全加算器を接続します。

