前回の記事で2進数4桁の加算器のロジック回路を紹介しましたが、実際にこの回路で動作させると、低速の動作では問題が起こらなくても、高速で動作させると、予期せぬ誤動作を招く場合があります。
例えば、NOT回路(図5)で説明します。理想的な入出力の波形は図6(a)のように方形波の入力に対して、反転した方形波の出力となるはずです。しかしながら、現実のロジック回路では図6(b)のように入力と出力は、LからHの立上がりと、HからLの立下がりが傾斜状に変化します。
 |
| 図5 NOT回路 |
出力の立上がりと立下りの傾斜時間は、出力上昇時間tTLH、出力下降時間tTHLといいます。また入力が変化してから、出力が変化するまでに時間遅れがあり、これを伝搬遅延時間といい、立上がりはtpLH、立下りはtpHLです。これらの値を電気的特性といい、メーカー資料で公開されています。
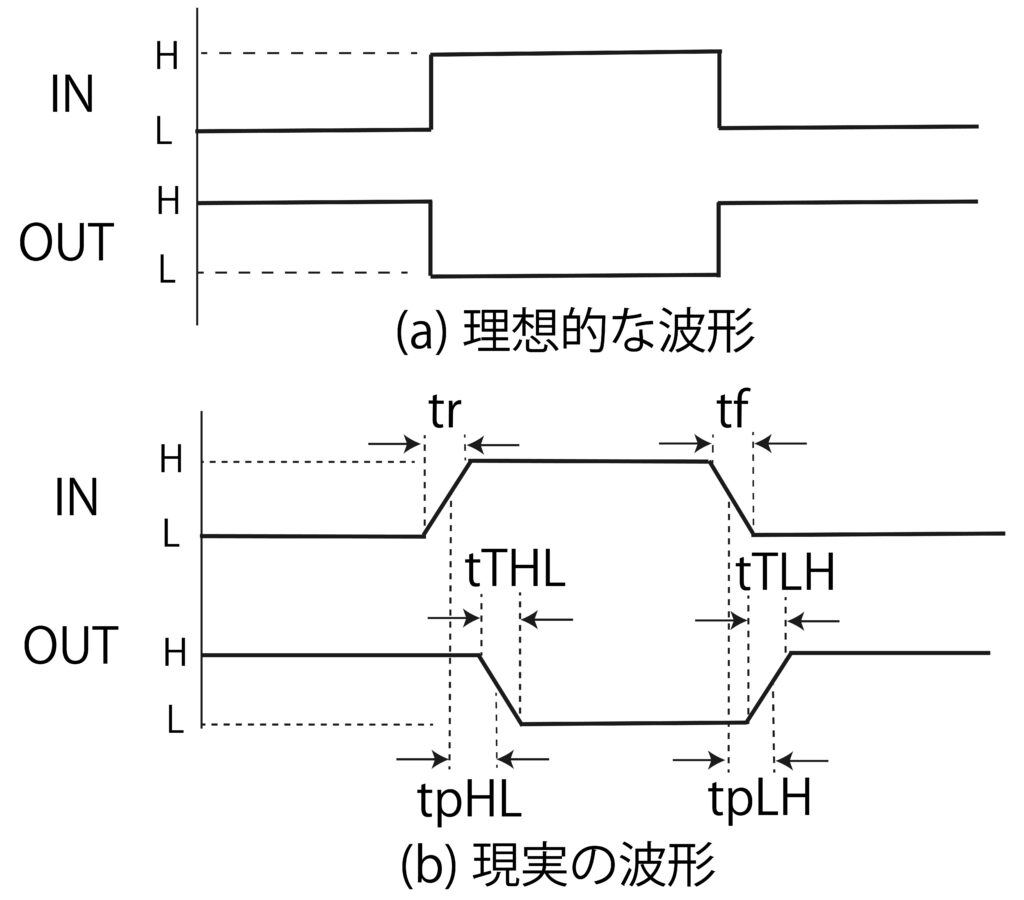 |
| 図6 ロジック回路における理想的波形と現実の波形 |
NOT回路TC74HC04APの電気的特性を抜粋したのが表1です。表1の単位はns(ナノ秒)で10億分の1秒という途方もなく小さい値ですが、近年ではCPUのクロック周波数が高速化し、回路の動作が早くなる傾向があり、表1のような小さな値でも無視できない場合があります。
| 項目 | 記号 | 最小 | 標準 | 最大 |
| 出力上昇、下降時間 | tTLH,tTHL | – | 8 | 15 |
| 伝搬遅延時間 | tpLH,tpHL | – | 9 | 15 |
また、表1はロジック回路1個についての遅延ですから、前述の加算器のように複数のロジック回路を直列に接続した場合には、その数だけ、信号波形の遅れが積算され、出力のタイミングがずれてしまいます。従って、ロジック回路の構成やソフトウェアによって、これを回避する手段を考えなければならない場合があります。